Geométricamente se pueden definir varios casos que están ligados a un triángulo en sí o en relación a la posición de una circunferencia.
Baricentro o Centroide: es el punto que se encuentra en la intersección de las medianas, y equivale al centro de gravedad.
Centros de circunferencias vinculadas:
- Circuncentro: es el centro de la circunferencia circunscrita, aquella que pasa por los tres vértices del triángulo. Se encuentra en la intersección de las mediatricesde los lados. Además, la circunferencia circunscrita contiene los puntos de intersección de la mediatriz de cada lado con las bisectrices que pasan por el vértice opuesto.
- Incentro: es el centro de la circunferencia inscrita, aquella que es tangente a los lados del triángulo. Se encuentra en la intersección de las bisectrices de los ángulos.
- Ortocentro: es el punto que se encuentra en la intersección de las alturas.
- Exincentros: son los centros de las circunferencias exinscritas. Se encuentra en la intersección de una bisectriz interior y dos bisectrices exteriores de los ángulos.
El único caso en que el baricentro, incentro, ortocentro y circuncentro coínciden es en el triángulo equilátero. Algunos de estos puntos caen en el interior, en el exterior o en el mismo triángulo, dependen de tipo. El ortocentro de un triángulo oblicuángulo está en el exterior; cuando se trata de un triángulo rectángulo isósceles el circuncentro no es sino el punto medio de la hipotenusa.
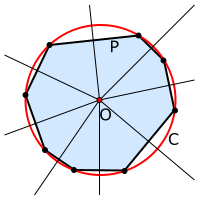
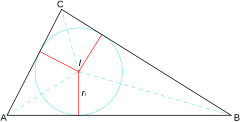
circuncentro incentro

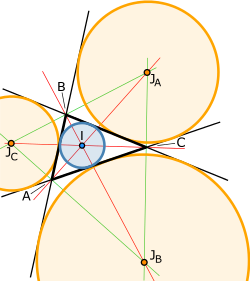
ortocentro exincentro


No hay comentarios:
Publicar un comentario