- La suma de las longitudes de dos de los lados de un triángulo es siempre mayor que la longitud del tercer lado.
- El valor de la base media de un triángulo (segmento que une dos puntos medios de dos lados) es igual a la mitad del lado paralelo.
- Los triángulos (polígonos de tres lados) son los únicos polígonos siempre convexos, no pueden ser cóncavos, dado que ninguno de sus tres ángulos puede superar los 180 grados o radianes.
- Para cualquier triángulo se verifica el Teorema del seno que establece: «Los lados de un triángulo son proporcionales a los senos de los ángulos opuestos»:

- Todo polígono convexo de n lados se puede descomponer en n-2 triángulos con interiores disjuntos, considerando un vértice del cual se trazan n-3 segmentos a los vértices no contiguos.
- Para cualquier triángulo se verifica el Teorema del coseno que establece: «El cuadrado de un lado es igual a la suma de los cuadrados de los otros lados menos el doble del producto de estos lados por el coseno del ángulo comprendido»:



- Para cualquier triángulo rectángulo, cuyos catetos miden a y b, y cuya hipotenusa mida c, se verifica el Teorema de Pitágoras:

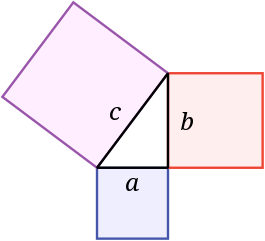
El teorema de Pitágoras gráficamente.
De la ecuación anterior se deducen fácilmente 3 fórmulas de aplicación práctica:



- Mediante rotación, traslación, simetría axial y simetría puntual la imagen de un triángulo es un triángulo congruente al propuesto.
- Dado un triángulo en el plano cartesiano se puede hallar la ecuación de una parábola circunscrita de eje horizontal o vertical.



No hay comentarios:
Publicar un comentario